| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- boj2352
- auto reload
- django
- Heterogeneous Graphs
- ngrok
- RGCN
- KG embedding
- cloudsql
- argocd
- 로깅 서버
- auto-reload
- knowledge graph
- cs224w
- npm7
- 영화 추천
- Graph Neural Network
- ML/DL
- Terragrunt
- IaaC
- Terraform
- SCP294
- the platform
- DevOps
- BigQuery
- GNNExplainer
- SCP 재단
- 영화 리뷰
- docker compose
- GNN
- 2352
- Today
- Total
Itmom's blog
Heterogeneous Graphs and RGCN (Relational GCN) 본문
1. Heterogenous Graphs란?
G = (V, E, R, T) 로 정의되며, 그래프의 각 요소들은 다음과 같다.
(1) node의 node type은 V에 속한다.
(2) edge의 edge type은 E에 속한다. edge의 요소로는 start node, end node 그리고 edge의 relation type이 있다.
아래 그림과 같은 graph가 대표적인 heterogenous graph라고 할 수 있다.

2. Relation GCN이란?
1) 정의
GCN (Graph Convolution Network)에서 message passing을 할 때 edge의 relation의 종류에 따라 다른 weight를 주어 message passing을 하도록 하는 것을 말한다.
2) 수식
$$ h_v^{(l+1)} = \sigma(\sum_{r \in R} \sum_{u \in N_v^r} \frac {1}{c_{v, r}} W_r^{(l)}h_u^{(l)} + W_0^{(l)}h_v^{(l)} ) $$
3) Scalability
각 relation은 L개의 layer가 있을 때, $$ d^{(l+1)} \times d^{(l)} $$ 크기의 matrix L개를 가지게 되는데, relation 개수가 증가함에 따라 parameter 수가 급격하게 증가하게 된다. 즉, overfitting이 발생할 수 있으며, 이를 통제하기 위해 다음 방법들을 고려할 수 있다.
(1) Block Diagonal Matrices
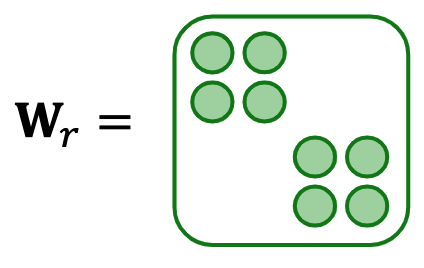
위 그림과 같이 행렬이 sparse할 경우, 대각선 부분에 있는 값들만 block 단위로 잘라 사용을 하는 기법이다. parameter 수를 줄일 수 있지만, diagonal에 있는 부분만 고려되다 보니 message passing을 할 때 근처에 있는 neuron과만 상호작용한다는 한계는 있다.
(2) Basis Learning
각 relation의 matrix를 basis transformation의 linear combination으로 고려한다. 수식으로 표현하면 다음과 같은 형태가 된다.
$$ W_r = \sum_{b=1}^B a_{rb} \cdot V_b $$
3. Knowledge Graphs (KG)
1) 정의
Knowledge Graph라고 불리는 heterogenous graph의 속성은 다음과 같다.
(1) node가 entity를 나타낸다.
(2) node가 node의 type으로 label 되어 있다.
(3) edge는 두 노드 사이의 관계를 나타낸다.
아래와 같은 bibliographic network가 kg의 한 예시이다.

2) KG Representation
KG의 edge들은 triplet (h, r, t)로 묘사될 수 있다.
h: head
r: relation
t: tail아이디어: (h, r)의 embedding이 t의 embedding과 최대한 유사해지도록 만드는 것이 목표로 각 속성의 embedding을 만들면 KG를 (h, r, t)로 묘사할 수 있다.
3) Relation Patterns
(1) Symmetric (Antisymmetric) Relations
$$ r(h,t) => r(t,h), (r(h,t) => \neg r(t,h)) \forall h, t $$
예시) 가족관계
(2) Inverse Relations
$$ r_2(h,t) => r_1(t,h) $$
예시) 선생님과 학생 관계
(3) Composition Relations
$$ r_1(x,y) \land r_2(y,z) => r_3(x,z) \forall x, y, z $$
예시) 내 엄마의 남편은 내 아빠다.
(4) 1-to-N relations
$$ r(h, t_1), r(h, t_2), ... , r(h, t_n) $$
예시) 내 학생들
4) KG embedding 기법들
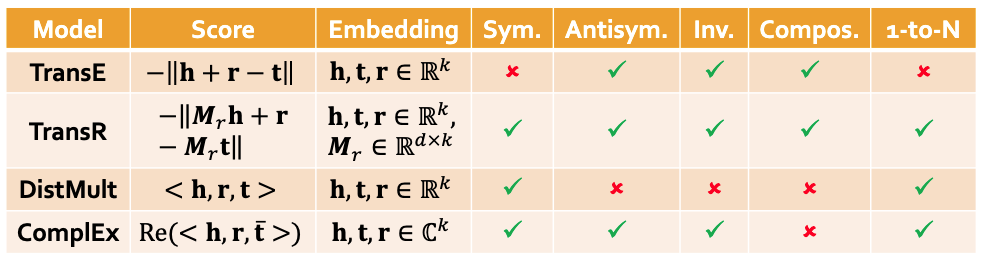
5) Answering Predictive Queries on KGs
Query의 종류: One-hop Queries, Path Queries, Conjunctive Queries
(1) 문제
KG가 incomplete하기 때문에, 모든 질문에 대한 대답을 구할 수 없음
-> KG completion을 하고 querying을 하면 될까?
-> completed KG는 dense graph라 시간복잡도가 급증함.
(2) 아이디어
아이디어: queries를 embedding하자.
Query embedding: q = h + r
q가 answer embedding t에 가까워지도록 query를 embedding하자.
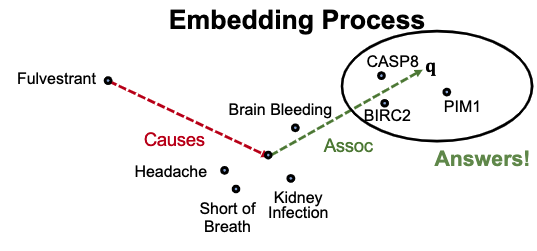
7) Query2Box: Reasoning over KGs Using Box embeddings
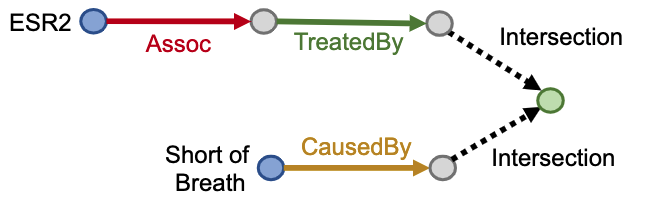
(1) 문제
위와 같이 intersection을 요구하는 query는 어떻게 처리할 수 있을까?
(2) 아이디어

box를 이용해 embedding을 수행하면 intersection 연산을 할 수 있다.
(3) Entity embeddings
entity를 zero-volume box처럼 볼 수 있다.
(4) Relation embeddings
relation은 box를 input으로 받아 새로운 box를 만들어낸다.
Projection Operator P: Box x Relation -> Box
Cen(q') = Cen(q) + Cen(r)
Off(q') = Off(q) + Off(r)
(5) Embed with Box Embedding
Intersection operator f: input으로 box들을 받아 box들의 intersection을 만들어낸다.
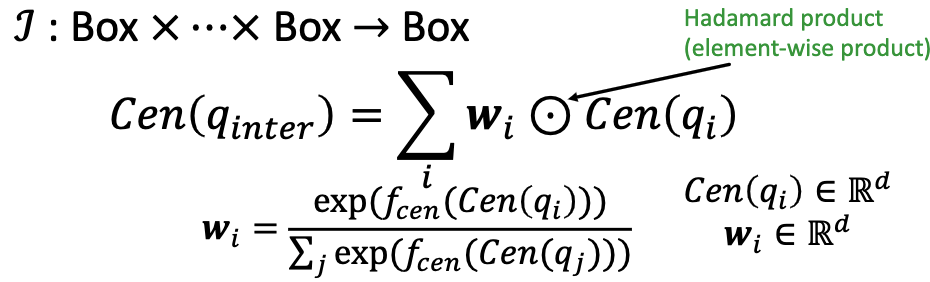

(6) Score function
원하는 point가 box안에 잘 내포되어 있다면, distance가 downweighted되어야 한다.
$$ d_box(q, v) = d_out(q, v) + \alpha \cdot d_in(q, v) $$
$$ f_q(v) = -d_box(q,v) $$
(7) 종합된 결과
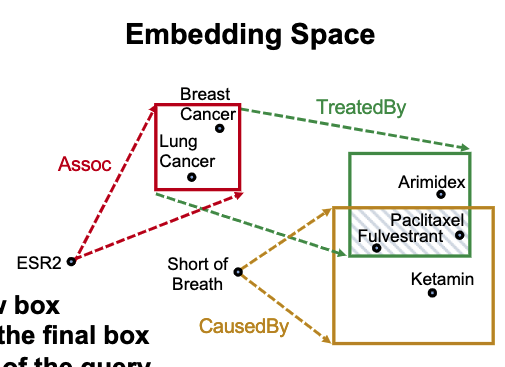
(8) And-or query
다음과 같이 4개의 query q1, q2, q3, q4에 대해 union operation을 하고자 할 때, 2-d에는 표현할 수 없음.
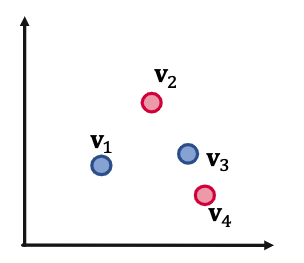
-> overlapping되는 대답이 없는 M개의 conjunctive query가 있을 때, 모든 OR query를 handling하기 위해 O(M) dimensionality가 필요하다.
-> union 연산을 나중에 처리하는 방식으로 해결 가능하다.
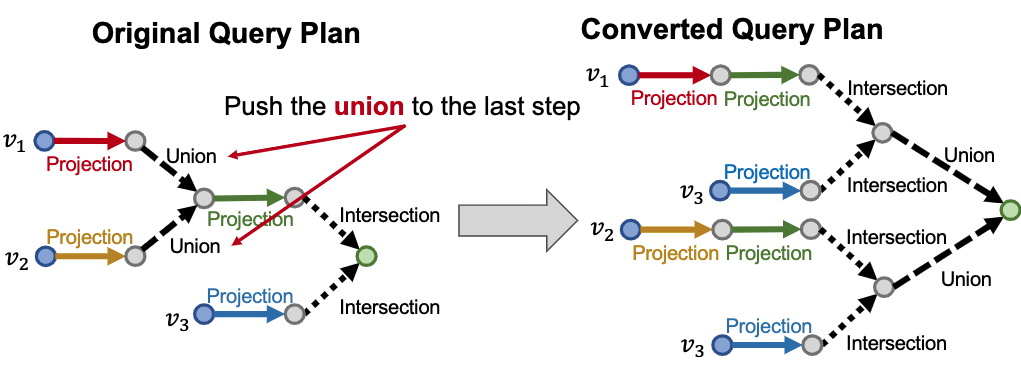
(9) 학습 방법
- Training graph로부터 sample query와 negative sample을 추출한다.
- query q를 embed한다.
- sample query와 negative sample query의 score를 계산한다.
- sample query에 대한 score를 maximize시키고, negative에 대한 score를 minimize시킬 수 있도록 loss를 최적화한다.
긴 글 읽어주셔서 감사합니다.
'Machine Learning' 카테고리의 다른 글
| Bayesian Optimization (0) | 2022.02.26 |
|---|---|
| GNN Explainer (0) | 2022.02.26 |
