| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Terragrunt
- RGCN
- ML/DL
- DevOps
- Terraform
- 영화 리뷰
- npm7
- argocd
- Graph Neural Network
- django
- GNN
- 2352
- Heterogeneous Graphs
- GNNExplainer
- auto reload
- BigQuery
- 영화 추천
- IaaC
- boj2352
- KG embedding
- SCP 재단
- 로깅 서버
- the platform
- SCP294
- auto-reload
- knowledge graph
- ngrok
- cloudsql
- docker compose
- cs224w
- Today
- Total
Itmom's blog
GNN Explainer 본문
참고) GNN에 대한 사전 지식이 필요합니다.
다음 강좌를 추천드립니다. Stanford CS224W
1. Background
GNN을 이용하여 학습을 시키고, 학습된 모델을 이용해 얻은 특정 node vector에 대한 embedding을 가지고 예측을 출력했을 때, 왜 그러한 예측 결과가 도출되었는지 알기 어렵다. 강력한 GNN의 성능을 설명할 수 있다는 수단이 없다는 점은 상당한 아쉬움으로 남는데, GNN Explainer 논문에서는 GNN에서 어떤 subgraph, 어떤 node feature가 특정 node vector에 대한 prediction을 생성하는데 큰 영향을 주었는가를 분석할 수 있는 framework를 제시한다.
딥러닝 모델의 예측 결과를 설명하기 위한 대표적인 방법으론, 임의로 생성한 n개의 sample에 대한 예측값을 이용해 선형 모델을 학습시켜 전체 모델을 설명하고자 하는 Local Interpretable Model-Agnostic Explanations (LIME)과 같은 방법과 모델 학습 과정에 직접 개입해 gradient를 직접 추적하는 등 연산 과정을 살펴보면서 중요한 정보를 얻어내는 방식을 꼽을 수 있다. 하지만, 두 방법 모두 gradient saturation로 인한 문제가 있었고, sailency maps를 출력해보았을 때, 일부 설명하지 못하는 부분들이 있는 것으로 확인되었다고 한다. GNN에 대해서 특화된 기법으로는, edge attention value를 사용하는 방법이 있지만, attention 메커니즘을 이용하는 특정 GNN 아키텍쳐에 대해서만 적용할 수 있다는 단점과 해당 attention sore는 모든 node에 대한 embedding을 생성할 때 적용되는 광범위한 score이기에 적용하기 어렵다는 단점이 있다. 이에, 논문에서는, 모델을 black box(입력을 넣으면 출력을 주지만, 중간 과정은 모르는 함수)로 보고, 모델을 이용해 여러가지 정보를 조사하는 post-hoc 방식을 취하고 있다. 구체적인 설명은 GNN Explainer 파트에 작성하였다.
2. GNN Explainer
1) Single-instance explanations
문제 정의: 특정 node vector의 prediction y를 생성하는데 가장 중요한 역할을 한 subgraph를 찾아내는 것
문제를 해결하기 위해, 논문에서는 다음과 같은 optimization framework를 제시하고 있다.
$${max_{G_S} MI(Y, (G_S, X_S)) = H(Y)-H(Y|G=G_S, X=X_S)}$$
예측값 y를 생성할 수 있는 전체 연산 Graph의 subgraph ${G_S}$ 를 규명하려는 의도를 확인할 수 있다. 여기서, ${H(Y)}$ 부분은 이미 예측된 값에 대한 엔트로피 값이기에 optimization 문제에서 constant로 취급 후 제거할 수 있다. 제거된 식은 다음과 같다.
$${H(Y|G=G_S, X=X_S) = -E_{Y|G_S,X_S}[{\log}P_{\phi}(Y|G=G_S, X=X_S)]}$$
objective function이 convex하다고 가정하면, 젠슨 부등식을 이용해 위 식을 아래와 같이 변환할 수 있다.
$${min_{G}H(Y|G=E_G[G_S], X = X_S)}$$
사실, neural network의 복잡함으로 인해 convexity assumtion은 잘못 되었다는 것을 알지만, 실험적으로, 위 objective을 최소화하는 것은 이따금 local minimum으로의 수렴을 만들어낸다는 것을 알고 있기에, 위 식을 사용할 수 있다.
위 식에서 ${E_G}$ 의 계산을 위해 mean-field variational approximation을 사용하고, G가 베르누이 분포를 따른다고 가정하면, gradient descent를 이용해 최적화할 수 있는 objective function을 도출할 수 있다.
$${min_M{-{\Sigma}{c=1}^{C}1[y=c]{\log}P{\phi}(Y=y|G=A_c{\odot}{\sigma}(M), X=X_c)}}$$
ajancency matrix에 부분적으로 mask를 취한 형태의 그래프를 이용해 prediction을 계산하고, 실제 prediction과의 loss를 도출해내 loss를 최소화할 수 있는 mask를 찾아내는 것이 목표라고 할 수 있다.
2) Joint learning of graph structural and node feature information
문제 정의: 특정 node vector의 prediction y를 생성하는데 가장 중요한 node feature를 찾아내는 것
중요한 subgraph를 찾아낼 때와 마찬가지로, subgraph를 고정시킨 상태에서 해당 subgraph에 속해있는 node vector에 mask를 씌우는 방식으로 objective function을 작성할 수 있다.
$${max_{G_S, G}MI(Y, (G_S, F))=H(Y)-H(Y|G=G_S, X=X_S^F)}$$
3) Multi-instance explanations through graph prototypes
문제 정의: 여러 output에 대한 explaination 도출. Ex) 특정 node set이 어떻게 라벨 c를 가지게 되었는가?
- Graph alignments: class c를 가지고 있는 node들 중, reference node를 선정한다. reference node에 대해 explanation을 생성한다. class c에 속한 다른 node들에 대해서도 반복한다.
- Prototypes: explanantion에 기반해 정렬된 adjacency matrix를 aggregate한다.
3. Experiment Result
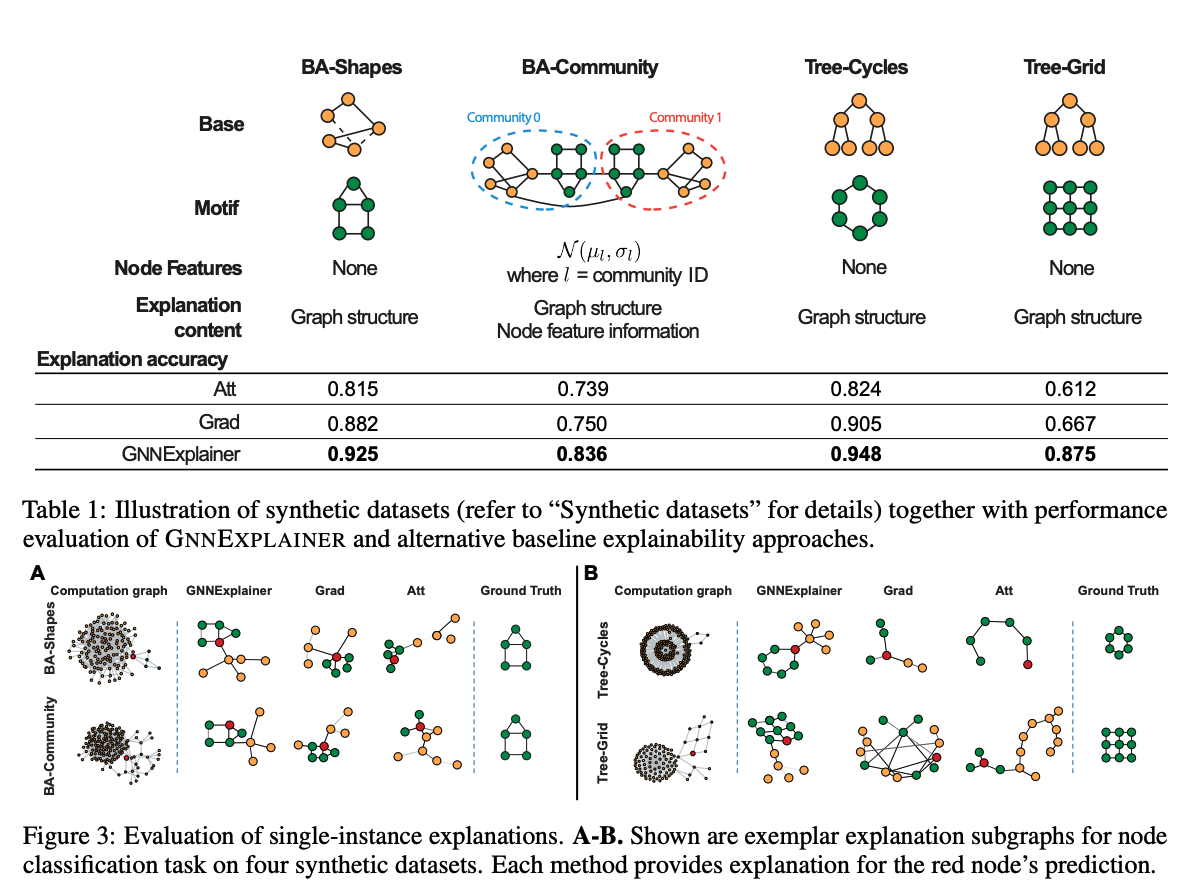
4. Implemetation
구현은 다음 링크를 참고했다.
우선, edge index와 node의 feature vector 정보를 이용해 subgraph를 생성한다. subgraph는 num_hops 값을 주어 연산 그래프의 hop값을 지정해줄 수도 있고, hop값을 주지 않는다면 model에 기반해 hop을 추정 후 graph를 생성합니다.
x, edge_index, mapping, hard_edge_mask, subset, kwargs = \
self.__subgraph__(node_idx, x, edge_index, **kwargs)그 후, model에 생성한 subgraph를 넣어 학습시키고, input node에 대해 출력을 만들고 난 뒤, actual value와 비교를 통해 loss 값을 만든다. loss값을 바탕으로 역전파를 하는 과정에서 node feature mask와 edge mask를 학습해 나간다.
if self.allow_edge_mask:
parameters = [self.node_feat_mask, self.edge_mask]
else:
parameters = [self.node_feat_mask]
optimizer = torch.optim.Adam(parameters, lr=self.lr)
if self.log: # pragma: no cover
pbar = tqdm(total=self.epochs)
pbar.set_description(f'Explain node {node_idx}')
for epoch in range(1, self.epochs + 1):
optimizer.zero_grad()
h = x * self.node_feat_mask.sigmoid()
out = self.model(x=h, edge_index=edge_index, **kwargs)
if self.return_type == 'regression':
loss = self.__loss__(mapping, out, prediction)
else:
log_logits = self.__to_log_prob__(out)
loss = self.__loss__(mapping, log_logits, pred_label)
loss.backward()
optimizer.step()'Machine Learning' 카테고리의 다른 글
| Bayesian Optimization (0) | 2022.02.26 |
|---|---|
| Heterogeneous Graphs and RGCN (Relational GCN) (0) | 2022.02.26 |

